Matemáticas aplicadas a la medicina

Por Carolina de la Caridad Bidó Bello
En el presente
ensayo hablaré sobre
la aplicación de las matemáticas en la medicina utilizando como ejemplo un modelo matemático
muy empleado en el área de la salud cardiaca,
el
electrocardiograma.
“El electrocardiograma es un examen que registra la actividad cardíaca del corazón” (Zieve, 2016). Este examen nos indica la actividad eléctrica y su conductividad a través del tejido cardíaco, lo que nos
permite conocer
la condición de nuestro corazón.
El electrocardiograma hace
uso de varios modelos matemáticos pero el más
interesante es conocido como la serie de Fourier, que es una expansión o aproximación de
una función periódica por
una serie infinita de funciones trigonométricas que utiliza
funciones de seno y coseno como
base.
Para poder entender mejor la serie de Fourier en el electrocardiograma hay que explicar cuáles son las ondas y que significan cada. Comencemos con la onda P que
representa la contracción de
la aurícula
izquierda, la
onda QRS representa
la despolarización de los ventrículos, la onda T representa la
polarización de los ventrículos.
Ya sabiendo
el significado de cada onda podemos explicar el uso de la serie de
Fourier.
La fórmula empleada en los electrocardiogramas es la siguiente:
Para poder comprender esta fórmula debemos saber que a0 es una constante, an representa la amplitud del coseno y
bn representa la
amplitud del seno.
Existen 2 tipos de ondas, la onda triangular que está representada por
QRS y
las
ondas parabólicas que son P y T (en caso de anomalía
se encuentra la onda U). Para calcular la
onda triangular se realizan 2 cálculos que
son la forma ascendente con f (t)=
-t
y la forma descendente con f (t)= t y para la forma parabólica se utiliza f (t)= -t² y para
calcular
las ondas parabólicas se utilizan los cálculos dependiendo
de qué onda sea, en la onda P f(t)= -ax²+b en la onda T
f(t)=-cx²+d. Pero en la onda Q se utiliza f(t)=-kt y
en
la onda S usamos f(t)= nt, ya que son las
que nos indican reposo.
El electrocardiograma es un medio diagnóstico utilizado a diario en la práctica médica,
ya que a través
del mismo
se pueden
identificar patologías cardiacas
como arritmias,
bloqueos e infartos que podrían poner
en peligro la vida de los pacientes.
Podemos concluir que las matemáticas tienen un gran desempeño
dentro
del área
de la
salud, ya que este no es el único modelo que participa en el electrocardiograma y
existen
otras aplicaciones importantes, entre las
que podemos mencionar desde
cosas básicas como
las medidas de las jeringas, los parámetros de laboratorio y en
las cirugías, como es el
caso especifico de la cirugía estereostáxica, entre
otras.
Ensayo escrito por Carolina
de la Caridad Bidó Bello 17-0241, estudiante de medicina, cursando la materia de Matematica I con el profesor Ramon Alberto Mena.
1. A.Chen,
M., & Zieve,
D. (2016, Noviembre
1). Electrocardiograma. Utilizado Noviembre
13,
2016, de MedlinePlus, https://medlineplus.gov/spanish/ency/article/003868.htm
2. La
matemática en relación con los
electrocardiogramas.
(2016). Utilizado Noviembre 13, 2016, de Prezi, https://prezi.com/k5j1adp-o6x5/la-matematica-en-relacion-con-los-electrocardiogramas/
3. Bourne,
M. (2004). Math of ECGs: Fourier series. Retrieved
November 13, 2016, de The InMath
4. Gan Ming De (2015, October 27). Design of a synthetic ECG signal based
on the
Fourier series.
Utilizado de https://www.youtube.com/watch?v=ASG1BJc25oY
5. Garcia,
G. (2016). Trigonometria en
Medicina. Usado Noviembre
20, 2016, de Prezi,
https://prezi.com/xqhc83yaczr3/trigonometria-en-medicina/



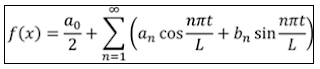




No hay comentarios.:
Publicar un comentario